解压轴题的关键是找出题目背后考核的知识点,会利用题干中的已经信息,分析出题目要考核用到的知识点。
在菱形ABCD中,∠BAD=60°.
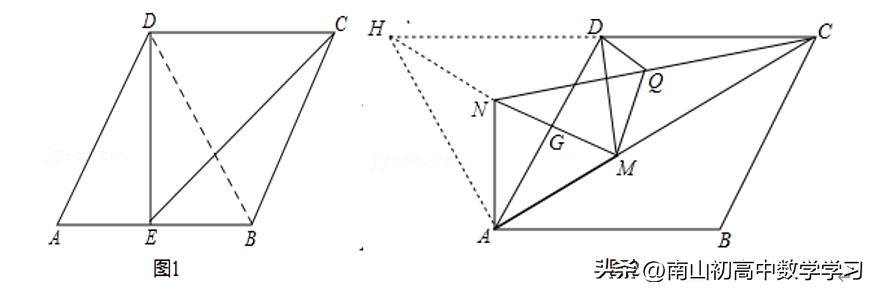
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.
解题思路分析方法:
1、 如何使用题干和前面小问的信息,题干的信息需要学会在各个小问中进行应用,如本题中的∠BAD=60°,有些压轴题的前面小问是后面小问的已知条件,这要看前面小问中的问题是否增加有新条件,本题中的一二问关联不大,都是只用到题干中的信息。
2、 已知信息的分析1:第一问中如何用活∠BAD=60°是关键,题干中的已知信息除了告诉四边形是菱形外,就是这个角的度数,由60°自然就联想到等边三角形的应用,通过连接BD就自然的构造出等边三角形,继而用到等边三角形的三线合一得出直角,从而根据勾股定理求出线段EC的长度。
3、 已知信息的分析2:第二问中需要证明的DM=2DQ,由两倍的关系根据初中的知识就联想到三角形的中位线性质,正好又有点Q是NC的中点,构造三角形的中位线方法解决线段的倍数关系。
解:(1)如图1,连接BD,则BD平分∠ABC,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=60°,
∴∠ABC=120°,
∴∠ABD=
∠ABC=60°,
∴△ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
∴DE⊥AB,
由勾股定理得:DE=2√3,
∵DC∥AB,
∴∠EDC=∠DEA=90°,
在Rt△DEC中,DC=4,
EC=2√7;
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,
∵AD=CD,
∴AD=DH,
∵CD∥AB,
∴∠HDA=∠BAD=60°,
∴△ADH是等边三角形,
∴AH=AD,∠HAD=60°,
∵△AMN是等边三角形,
∴AM=AN,∠NAM=60°,
∴∠HAN+∠NAG=∠NAG+∠DAM,
∴∠HAN=∠DAM,
在△ANH和△AMD中,AH=AD,∠HAN=∠DAM,AN=AM
∴△ANH≌△AMD(SAS),
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是△CHN的中位线,
∴HN=2DQ,
∴DM=2DQ.